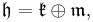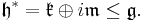Hermitian symmetric space

In mathematics, a Hermitian symmetric space is a Kähler manifold M which, as a Riemannian manifold, is a Riemannian symmetric space. Equivalently, M is a Riemannian symmetric space with a parallel complex structure with respect to which the Riemannian metric is Hermitian. The complex structure is automatically preserved by the isometry group H of the metric, and so M is a homogeneous complex manifold.

Some examples are complex vector spaces and complex projective spaces, with their usual Hermitian metrics and Fubini-Study metrics, and the complex unit balls with suitable metrics so that they become complete and Riemannian symmetric. The compact Hermitian symmetric spaces are projective varieties, and admit a strictly larger Lie group G of biholomorphisms with respect to which they are homogeneous: in fact, they are generalized flag manifolds, i.e., G is semisimple and the stabilizer of a point is a parabolic subgroup P of G. Among (complex) generalized flag manifolds G/P, they are characterized as those for which the nilradical of the Lie algebra of P is abelian. The non-compact Hermitian symmetric spaces can be realized as bounded domains in complex vector spaces.

Hermitian symmetric spaces are used in the construction of the holomorphic discrete series representations of semisimple Lie groups.

Compact Hermitian symmetric spaces

The irreducible compact Hermitian symmetric spaces H/K are classified as follows.

G H K complex dimension geometric interpretation
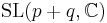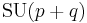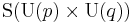\mathrm{SL}(p%2Bq,\mathbb{C}) \mathrm{SU}(p%2Bq)\, \mathrm{S}(\mathrm{U}(p) \times \mathrm{U}(q)) pq Grassmannian of complex p-dimensional subspaces of 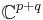\mathbb{C}^{p%2Bq}
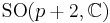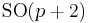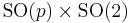\mathrm{SO}(p%2B2,\mathbb{C}) \mathrm{SO}(p%2B2)\, \mathrm{SO}(p) \times \mathrm{SO}(2) p Grassmannian of oriented real 2-dimensional subspaces of 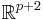\mathbb{R}^{p%2B2}
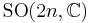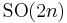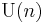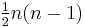\mathrm{SO}(2n,\mathbb C) \mathrm{SO}(2n)\, \mathrm{U}(n)\, \tfrac 12 n(n-1) Space of orthogonal complex structures on 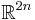\mathbb{R}^{2n}
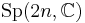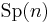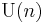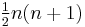\mathrm{Sp}(2n,\mathbb C)\, \mathrm{Sp}(n)\, \mathrm{U}(n)\, \tfrac 12 n(n%2B1) Space of complex structures on 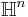\mathbb{H}^n compatible with the inner product
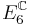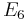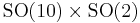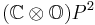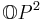E_6^{\mathbb C}\, E_6\, \mathrm{SO}(10)\times\mathrm{SO}(2) 16 Complexification (\mathbb{C}\otimes\mathbb{O})P^2 of the Cayley projective plane \mathbb{O}P^2
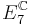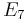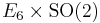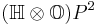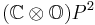E_7^{\mathbb C} E_7\, E_6\times\mathrm{SO}(2) 27 Space of symmetric submanifolds of Rosenfeld's projective plane (\mathbb{H}\otimes\mathbb{O})P^2 which are isomorphic to (\mathbb{C}\otimes\mathbb{O})P^2

In terms of the classification of compact Riemannian symmetric spaces, the Hermitian symmetric spaces are the four infinite series AIII, BDI with p = 2 or q = 2, DIII and CI, and two exceptional spaces, namely EIII and EVII.

The realization of H/K as a generalized flag variety G/P is obtained by taking G as in the table (a complexification of H) and P equal to the semidirect product of L with the complexified isotropy representation of K, where L (the Levi factor of P) is the complexification of K.

At the Lie algebra level, there is a symmetric decomposition

\mathfrak h = \mathfrak k\oplus\mathfrak m,

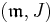where (\mathfrak m,J) is a real vector space with a complex structure J, whose complex dimension is given in the table. Correspondingly, there is a graded Lie algebra decomposition

\mathfrak g = \mathfrak m^{-}\oplus\mathfrak l\oplus\mathfrak m^{%2B}

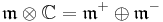where \mathfrak m\otimes\mathbb C= \mathfrak m^{%2B}\oplus\mathfrak m^{-} is the decomposition into +i and −i eigenspaces of J and 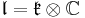\mathfrak l=\mathfrak k\otimes\mathbb C. The Lie algebra of P is the semidirect product 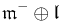\mathfrak m^{-}\oplus\mathfrak l. It follows that the exponential image of 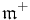\mathfrak m^{%2B} modulo P realizes the complex vector space 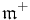\mathfrak m^{%2B} as a dense open subset of G/P.

Non-compact Hermitian symmetric spaces

As with symmetric spaces in general, each compact Hermitian symmetric space H/K has a noncompact dual H*/K obtained by replacing H with the Lie group H* in G whose Lie algebra is

\mathfrak h^* = \mathfrak k \oplus i\mathfrak m\leq\mathfrak g.

However, whereas the natural map from H/K to G/P is an isomorphism, the natural map from H*/K to G/P is only an injection. In fact its image lies in the exponential image of 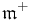\mathfrak m^%2B and the corresponding domain in 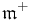\mathfrak m^%2B is bounded (this is the Harish-Chandra embedding theorem). The biholomorphism group of H*/K is equal to its isometry group H*.

A bounded domain Ω in a complex vector space (i.e., Ω is an open subset whose closure is compact with respect to the standard topology) is said to be a bounded symmetric domain if for every x in Ω, there is a biholomorphism σx of Ω for which x is an isolated fixed point. Given such a domain Ω, the Bergman kernel defines a metric on Ω, the Bergman metric, for which every biholomorphism is an isometry. This realizes Ω as a Hermitian symmetric space of noncompact type.

References